第 1 章 神经网络如何工作

1.2 一台简单的预测机

更多又去的问题是没有一个简单的数学公式将输出和输入关联起来的。这就是我们需要诸如神经网络这样相对成熟而复杂的方法的原因。

关键点

• 当我哦们不能精确知道一些事情如何运作时，我们可以尝试使用模型来估计其运作方式，在模型中，包括了我们可以调整的参数。
• 改进这些模型的一种好方法是，基于模型和已知真实示例之间的比较，得到模型偏移的误差值，调整参数。

1.4 训练简单的分类器

关键点

• 使用朴素的调整方法会出现一个问题，即改进后的模型只与最后一次训练样本最匹配，“有效地”忽略了所有以前的训练样本。解决这个问题的一种好方法是使用学习率，调解改进速度，这样单一的训练样本就不能主导整个学习过程。
• 来自真实世界的训练样本可能充满噪声或包含错误。适度更新有助于限制这些错误样本的影响。

1.5 有时候一个分类器不足以求解问题

如果出现的是由 XOR 函数支配的训练数据，那么一个简单的线性分类器无法学习到布尔 XOR 函数。

在一些任务中，根本性问题不是线性可分的，也就是说单一的一条直线于事无补，而我们希望神经网络能够解决此类的任务。

也就是说，我们可以使用多个分类器一起工作。这是神经网络的核心思想。

关键点

• 如果数据本身不是由单一线性过程支配，那么一个简单的线性分类器不能对数据进行划分。例如，由逻辑 XOR 运算符支配的数据说明了这一点。
• 但是解决方案很容易，你只需要使用多个线性分类器来划分由单一直线无法分离的数据。

1.6 神经元 —— 大自然的计算机器

生物神经元与简单的线性函数不一样，不能简单地对输入做出的响应，生成输出。

观察表明，神经元不会立即反应，而是会抑制输入，直到输入增强，强大到可以触发输出。你可以这样认为，在产生输出之前，输入必须达到一个阈值。

直观上，这是有道理的 —— 神经元不希望传递微小的噪声信号，而只是传递有意识的明显信号。

虽然这个函数接受了输入信号，产生了输出信号，但是我们要将某种称为激活函数的阈值考虑在内。在数学上，有许多激活函数可以达到这样的效果。一个简单的阶跃函数可以实现这种效果。

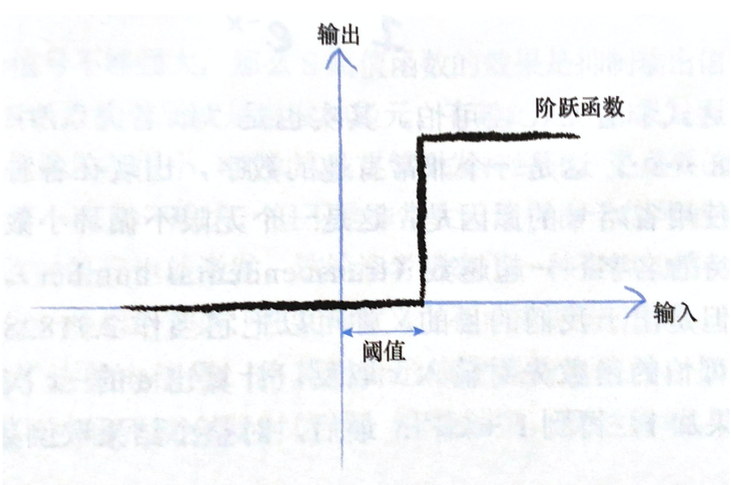
输入达到阈值时，神经元就激发了。

我们可以改进阶跃函数。下图所示的 S 形函数成为 S 函数（sigmoid function）。这个函数，比起冷冰冰、硬邦邦的阶跃函数要相对平滑，这使得这个函数更自然、更接近现实。自然界很少有冰冷尖锐的边缘！

… 生物神经元可以接受许多输入，而不仅仅是一个输入。… 对于所有这些输入，… 我们只需对它们进行相加，得到最终总和，作为 S 函数的输入，然后输出结果。这实际上反映了神经元的工作机制。

如果组合信号不够强大，那么 S 阈值函数的效果是抑制输出信号。如果总和 x 足够大，S 函数的效果就是激发神经元。有趣的是，如果只有其中一个输入足够大，其他输入都很小，那么这也足够激发神经元。更重要的是，如果其中一些输入，单个而言一般大，但不是非常大，这样由于信号的组合足够大，超过阈值，那么神经元也能激发。这给读者带来了一种直观的感觉，即这些神经元也可以进行一些相对复杂、在某种意义上有点模糊的计算。

树突收集了这些电信号，将其组合形成更强的电信号。如果信号足够强，超过阈值，神经元就会发射信号，沿着轴突，到达终端，将信号传递给下一个神经元的树突。下图显示了使用这种方式连接的若干神经元。

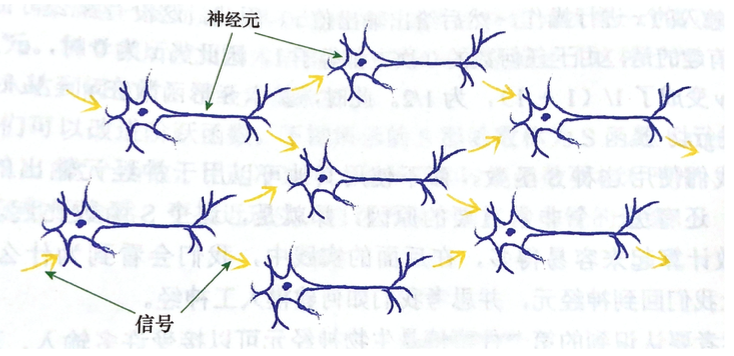
需要注意的一点是，每个神经元接受来自其之前多个神经元的输入，并且如果神经元被激发了，它也同时提供信号给更多的神经元。

将这种自然形式复制到人造模型的一种方法是，构建多层神经元，每一层中的神经元斗鱼在其前后层的神经元互相连接。下图详细描述了这种思想。

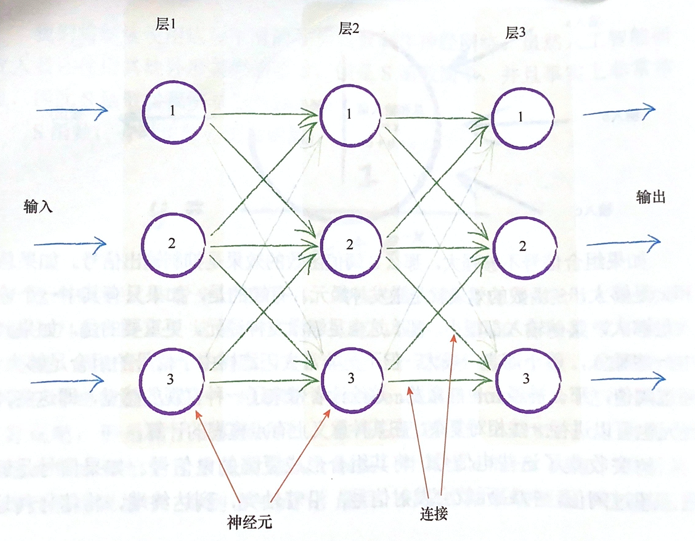
关键点

• 相比于传统的计算机系统，生物大脑对损坏和不完善信号具有难以置信的弹性。
• 由互相连接的神经元组成的生物大脑是人工神经网络的灵感来源。

1.7 在神经网络中追踪信号

权重是神经网络进行学习的内容，这些权重持续进行优化，得到越来越好的结果。

1.8 平心而论，矩阵乘法大有用途

… 矩阵在两个方面帮助了我们。首先，矩阵允许我们压缩所有这些计算，把它们变成一种非常简单的缩写形式。… 第二个好处是，许多计算机编程语言理解如何与矩阵一起工作，计算机编程语言能够认识到实际的工作是重复性的，因此能够高效高速地进行计算。

第一个数字代表行，第二个数字代表列，这是约定

一些人使用方括号表示矩阵，另一些人 … 使用圆括号表示矩阵

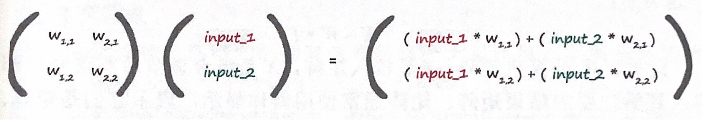
第一个矩阵包含两层节点之间的权重。第二个矩阵包含第一层输入层的信号。通过两个矩阵相乘，我们得到的答案是输入到第二层节点组合调节后的信号。

关键点

• 通过神经网络向前馈送信号所需的大量运算可以表示为矩阵乘法。
• 不管神经网络的规模如何，将输入输出表达为矩阵乘法，使得我们可以更简洁地进行书写。
• 更重要的是，一些计算机编程语言理解矩阵计算，并认识到潜在的计算方法的相似性。这允许计算机高速高效地进行这些计算。

1.9 使用矩阵乘法的三层神经网络示例

… 第一层为输入层，最后一层为输出层，中间层我们称之为隐藏层。… 中间层的输出不需要很明显地表示为输出，因此我们称之为“隐藏”层。

将神经网络的输出值与训练样本中的输出值进行比较，计算出误差。我们需要使用这个误差值来调整神经网络本身，进而改进神经网络的输出值。

1.10 学习来自多个节点的权重

… 我们在两件事情上使用了权重。第一件事情，在神经网络中，我们使用权重，将信号从输入向前传播到输出层。… 第二件事情，我们使用权重，将误差从输出向后传播到网络中。我们称这种方法为反向传播

1.12 反向传播误差到更多层中

如果神经网络具有多个层，那么我们就从最终输出层往回工作，对吗诶一层重复应用相同的思路。… 你明白为什么我们称之为误差的反向传播了。

下图详细阐释了在一个简单的具有实际数字的 3 层网络中，误差如何向后传播。

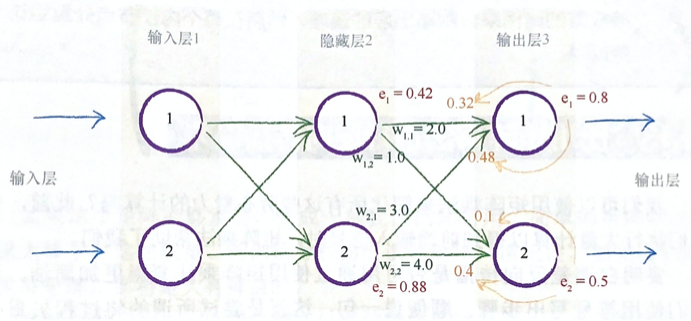
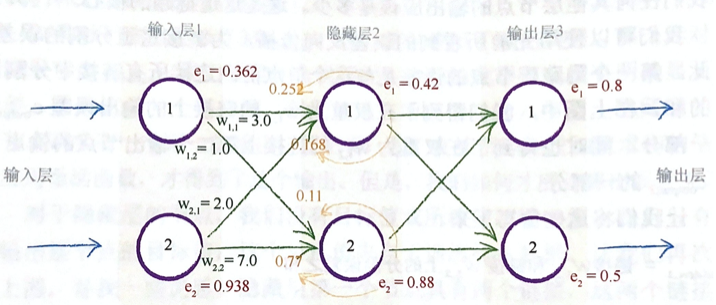
关键点

• 神经网络通过调整链接权重进行学习。这种方法由误差引导，误差就是训练数据所给出正确答案和实际输出之间的差值。
• 简单地说，在输出节点处的误差等于所需值与实际值之间的差值。
• 然而，与内部节点相关联的误差并不显而易见。一种方法是按照链接权重的比例来分割输出层的误差，然后在每个内部节点处重组这些误差。

1.13 使用矩阵乘法进行反向传播误差

… 矩阵沿对角线进行了翻转，因此现在右上方的元素变成了左下方的元素，左下方的元素变成了右上方的元素。我们称此为转置矩阵，记为 w^T。

即使矩阵的行数和列数不同，也是可以进行转置的。

虽然这样做看起来不错，但是将归一化因子切除，我们做得正确吗？实践证明，这种相对简单的误差信号反馈方式，与我们先前相对复杂的方式一样有效。… 如果这种相对简单的方式行之有效，那么我们就应该坚持这种方法。

关键点

• 反向传播误差可以表示为矩阵乘法。
• 无论网络规模大小，这使我们能够简洁地表达反向传播误差，同时也允许理解矩阵计算的计算机语言更高效、更快速地完成工作。
• 这意味着前向馈送信号和反向传播误差都可以使用矩阵计算而变得高效。

1.14 我们实际上如何更新权重

在数学上，这种方法成为梯度下降（gradient descent），你可以明白这是为什么吧。在你迈出一步之后，再次观察周围的地形，看看你下一步往哪个方向走，才能更接近目标，然后，你就往那个方向走出一步。你一直保持这种方式，直到非常欣喜地到达了山底。梯度是指地面的坡度。你走的方向是最陡的坡度向下的方向。

现在，想象一下，这个复杂的地形是一个数学函数。梯度下降法给我们带来一种能力，即我们不必完全理解复杂的函数，从数学上对函数进行求解，就可以找到最小值。如果函数非常困难，我们不能用代数轻松找到最小值，我们就可以使用这个方法来代替代数方法。当然，由于我们采用步进的方式接近答案，一点一点地改进所在的位置，因此这可能无法给出精确解。但是，这比得不到答案要好。总之，我们可以使用更小的步子朝着实际的最小值方向迈进，优化答案，知道我们对于所得到的的精度感到满意为止。

我们要改变步子大小，避免超调，这样就会避免在最小值的地方来回反弹，这是一个必要的优化。…如果我们调解步长，与梯度的大小成比例，那么在接近最小值时，我们就可以采用小步长。这一假设的基础是，当我们接近最小值时，斜率也变得平缓了。对于大多数光滑的连续函数，这个假设是合适的。但是对于有时突然一跃而起、有时突然急剧下降的锯齿函数而言，也就是说存在数学家所说的间断点，这不是一个合适的假设。

关键点

• 梯度下降法是求解函数最小值的一种很好的办法，当函数非常复杂困难，并且不能轻易使用数学代数求解函数时，这种方法却发挥了很好的作用。
• 更重要的是，当函数有很多参数，一些其他方法不切实际，或者会得出错误答案，这种方法依然可以适用。
• 这种方法也具有弹性，可以容忍不完善的数据，如果我们不能完美地描述函数，或我们偶尔意外地走错了一步，也不会错得离谱。

更新后的权重 w_i,j 是由刚刚得到的误差斜率取反来调整旧的权重而得到的。正如我们先前所看到的，如果斜率为正，我们希望减小权重，如果斜率为负，我们希望增加权重，因此，我们要对斜率取反。符号 α 是一个因子，这个因子可以调节这些变化的强度，确保不会超调。我们通常称这个因子为学习率。

关键点

• 神经网络的误差是内部链接权重的函数。
• 改进神经网络，意味着通过改变权重减少这种误差。
• 直接选择合适的权重太难了。另一种方法是，通过误差函数的梯度下降，采取小步长，迭代地改进权重。所迈出的每一步的下降方向都是在当前位置向下斜率最大的方向，这就是所谓的梯度下降。
• 使用微积分可以很容易地计算出误差斜率。

1.15 权重更新成功范例

… 权重经过成百上千次的迭代，最终会确定下来，达到一种布局，这样训练有素的神经网络就会生成与训练样本中相同的输出。

1.16 准备数据

1.16.1 输入

权重的改变取决于激活函数的梯度。小梯度意味着限制神经网络学习的能力。这就是所谓的饱和神经网络。

关键点

• 如果输入、输出和初始权重数据的准备与网络设计和实际求解的问题不匹配，那么神经网络并不能很好地工作。
• 一个常见的问题是饱和。在这个时候，大信号（这有时候是由大权重带来的）导致了应用在信号上的激活函数的斜率变得非常平缓。这降低了神经网络学习到更好权重的能力。
• 另一个问题是零值信号或零值权重。这也可以使网络丧失学习更好权重的能力。
• 内部链接的权重应该是随机的，值较小，但要避免零值。如果节点的传入链接较多，有一些人会使用相对复杂的规则，如减小这些权重的大小。
• 输入应该调整到较小值，但不能为零。一个常见的范围为 0.010.99，或 -1.01.0，使用哪个范围，取决于是否匹配了问题。
• 输出应该在激活函数能够生成的值的范围内。逻辑 S 函数是不可能生成小于等于 0 或大于等于 1 的值。将训练目标值设置在有效的范围之外，将会驱使产生越来越大的权重，导致网络饱和。一个合适的范围为 0.01~0.99。

第 2 章 使用 Python 进行 DIY

2.5 手写数字的数据集 MNIST

2.5.1 准备 MNIST 训练数据

对于一个问题，应该选择多少个隐藏层节点，并不存在一个最佳方法。同时，我们也没有最佳方法选择需要几层隐藏层。就目前而言，最好的办法是进行实验，直到找到适合你要解决的问题的一个数字。

2.5.4 一些改进：调整学习率

对于学习率存在一个甜蜜点。

2.5.5 一些改进：多次运行

接下来可以做的改进，是使用数据集，重复多次进行训练。

有些人把训练一次称为一个世代。因此，具有 10 个世代的训练，意味着使用整个训练数据集运行程序 10 次。 … 这是值得的，原因是通过提供更多爬下斜坡的机会，有助于在梯度下降过程中进行权重更新。

有人可能会注意到，太多的训练实际上会过犹不及，这是由于网络过度拟合训练数据，因此网络在先前没有见到过的新数据上表现不佳。不仅是神经网络，在各种类型的机器学习中，这种过度拟合也是需要注意的。

直观上，如果你打算使用更长的时间（多个世代）探索梯度下降，那么你可以承受采用较短的步长（学习率），并且在总体上可以找到更好的路径，这是有道理的。

要正确、科学地做到这一点，就必须为每个学习率和世代组合进行多次实验，尽量减少在梯度下降过程中的随机性的影响。

2.5.6 改变网络形状

隐藏层是发生学习过程的层次。请记住，输入节点只需引入输入信号，输出节点只要送出神经网络的答案，是隐藏层（可以多层）进行学习，将输入转变为答案。这是学习发生的场所。事实上，隐藏层节点前后的链接权重具有学习能力。

如果隐藏层节点太少，比如说 3 个，那么你可以想象，这不可能有足够的空间让网络学习任何知识，并将所有输入转换为正确的输出。… 计算机科学家称这种限制为学习容量。

随着增加隐藏层节点的数量，结果有所改善，但是不显著。由于增加一个隐藏层节点意味着增加了到前后层的每个节点的新网络链接，这一切都会产生额外较多的计算，因此训练网络所用的时间也显著增加了！因此，必须在可容忍的运行时间内选择某个数目的隐藏层节点。

第 3 章 趣味盎然

3.3 创建新的训练数据：旋转图像

我们说“特定的神经网络架构”，意思是在每一层节点数目的选择、隐藏层的选择和激活函数的选择等。

附录 A 微积分简介

A.1 一条平直的线

微积分探讨的是，建立关系以表示一种事物如何随着其他事物的变化而变化。

A.2 一条斜线

请记住，直线的一般形式为 y = ax + b，其中 a 是斜率或梯度。

A.4 手绘微积分

在曲线任何点处的变化率，就是曲线在该点的斜率。

A.7 模式

幂规则：若 n 是任意实数，对于函数 f(x) = x^n, (x^n)’ = n * x^(n-1).

y = axⁿ => δy / δx = nax^n-1

A.8 函数的函数

链式法则：若 y = f(g(x)), 则 y’ = f’(g(x)) * g’(x).

δf / δx = δf/δy * δy/δx