你不能比较苹果和橙子。或者你可以吗?像 Milvus 这样的向量数据库允许你比较任何你可以向量化的数据。你甚至可以在你的 Jupyter Notebook 中做到这一点。但是 向量相似性搜索 是如何工作的呢?
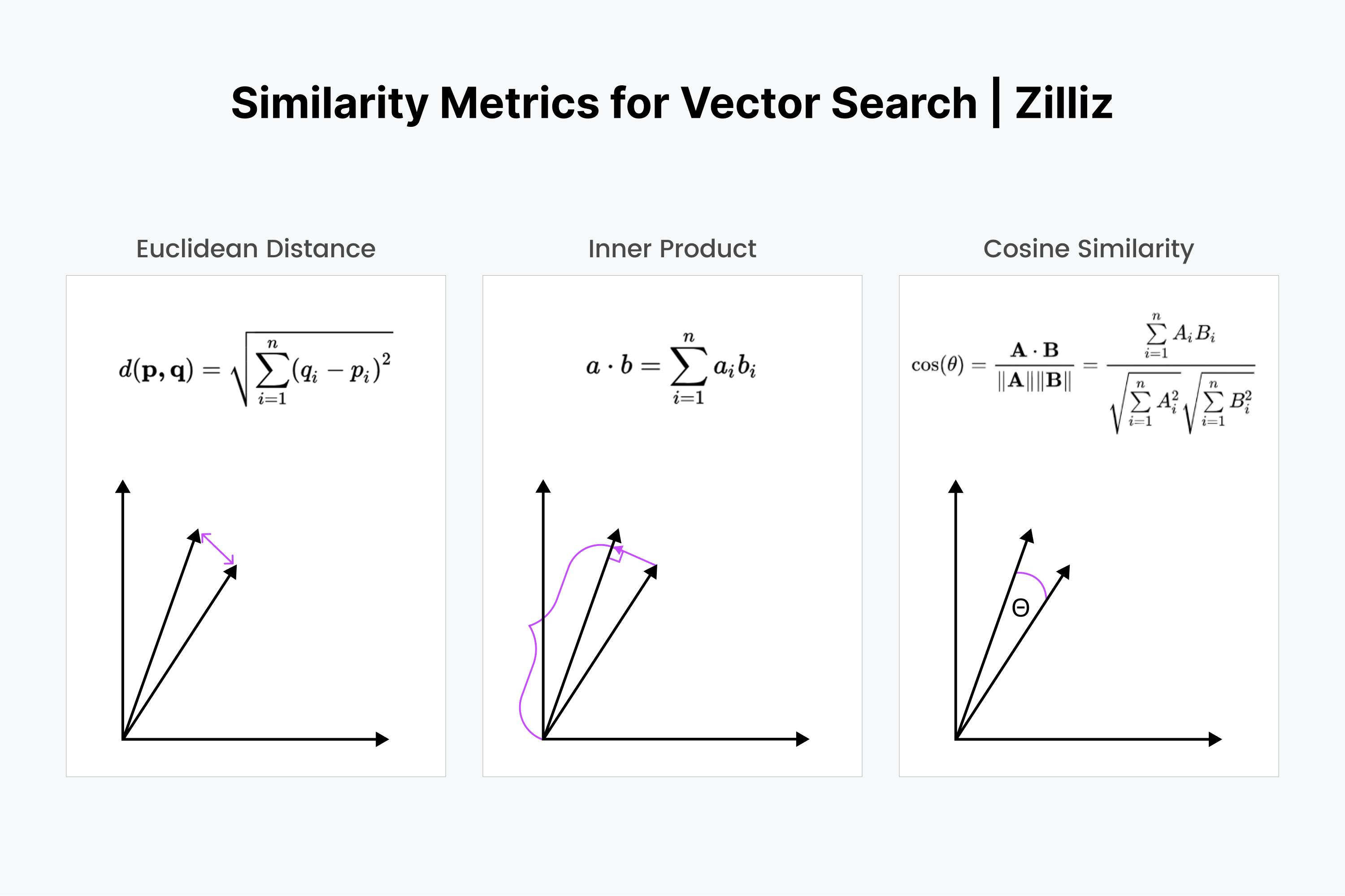
向量搜索有两个关键的概念组成部分:索引和距离度量。一些流行的向量索引包括 HNSW、IVF 和 ScaNN。主要的三种距离度量是:L2 或欧几里得距离、余弦相似度和内积。其他度量还有可用于二进制向量的汉明距离和杰卡德系数。
在这篇文章中,我们将涵盖:
- 向量相似度度量
- L2 或欧几里得距离
- L2 距离是如何工作的?
- 何时应该使用欧几里得距离?
- 余弦相似度
- 余弦相似度是如何工作的?
- 何时应该使用余弦相似度?
- 内积
- 内积是如何工作的?
- 何时应该使用内积?
- 其他有趣的向量相似度或距离度量
- 汉明距离
- 杰卡德指数
- 向量相似度搜索度量总结
向量相似度度量
向量可以表示为数字列表或方向和大小。为了更容易理解,你可以将向量想象为指向特定方向的线段。
- L2或欧几里得度量 是两个向量之间的“斜边”度量。它衡量了向量线条结束点之间的距离大小。
- 余弦相似度 是指它们相交时线之间的夹角。
- 内积 是将一个向量投影到另一个向量上的操作。直观地说,它同时衡量了向量之间的距离和角度。
L2 或欧几里得距离
L2 或欧几里得距离是最直观的距离度量。我们可以将其想象为两个物体之间的空间量。例如,你的屏幕离你的脸有多远。
L2 或欧几里得距离是如何工作的?

那么,我们已经想象了 L2 距离在空间中是如何工作的;在数学中它是如何工作的呢?让我们首先将两个向量想象为一列数字。将这些数字列表上下对齐,然后向下相减。接着,将所有结果平方并相加。最后,取平方根。
Milvus 跳过了平方根步骤,因为平方根处理前后的排名顺序是相同的。这样,我们可以省去一个操作步骤并得到相同的结果,降低延迟和成本,提高吞吐量。下面是一个欧几里得或 L2 距离如何工作的例子。
d(Queen, King) = $$\sqrt{(0.3-0.5)^2 + (0.9-0.7)^2}$$
= $$\sqrt{(-0.2)^2 + (0.2)^2}$$
= $$\sqrt{0.04 + 0.04}$$
= $$\sqrt{0.08}$$ ≈ 0.28
何时应该使用 L2 或欧几里得距离?
使用欧几里得距离的一个主要原因是当您的向量具有不同的大小(magnitudes)时。您主要关心的是您的词汇在空间中或语义上的距离有多远。
余弦相似度
我们使用“余弦相似度”或“余弦距离”来表示两个向量之间的方向差异。例如,你需要转多少度才能面向前门?
有趣且实用的事实:尽管“相似度”和“距离”两个词单独来看有不同的含义,但在它们前面加上“余弦”后会使它们的意思几乎相同!这是语义相似性的又一个例子。
余弦相似度是如何工作的?
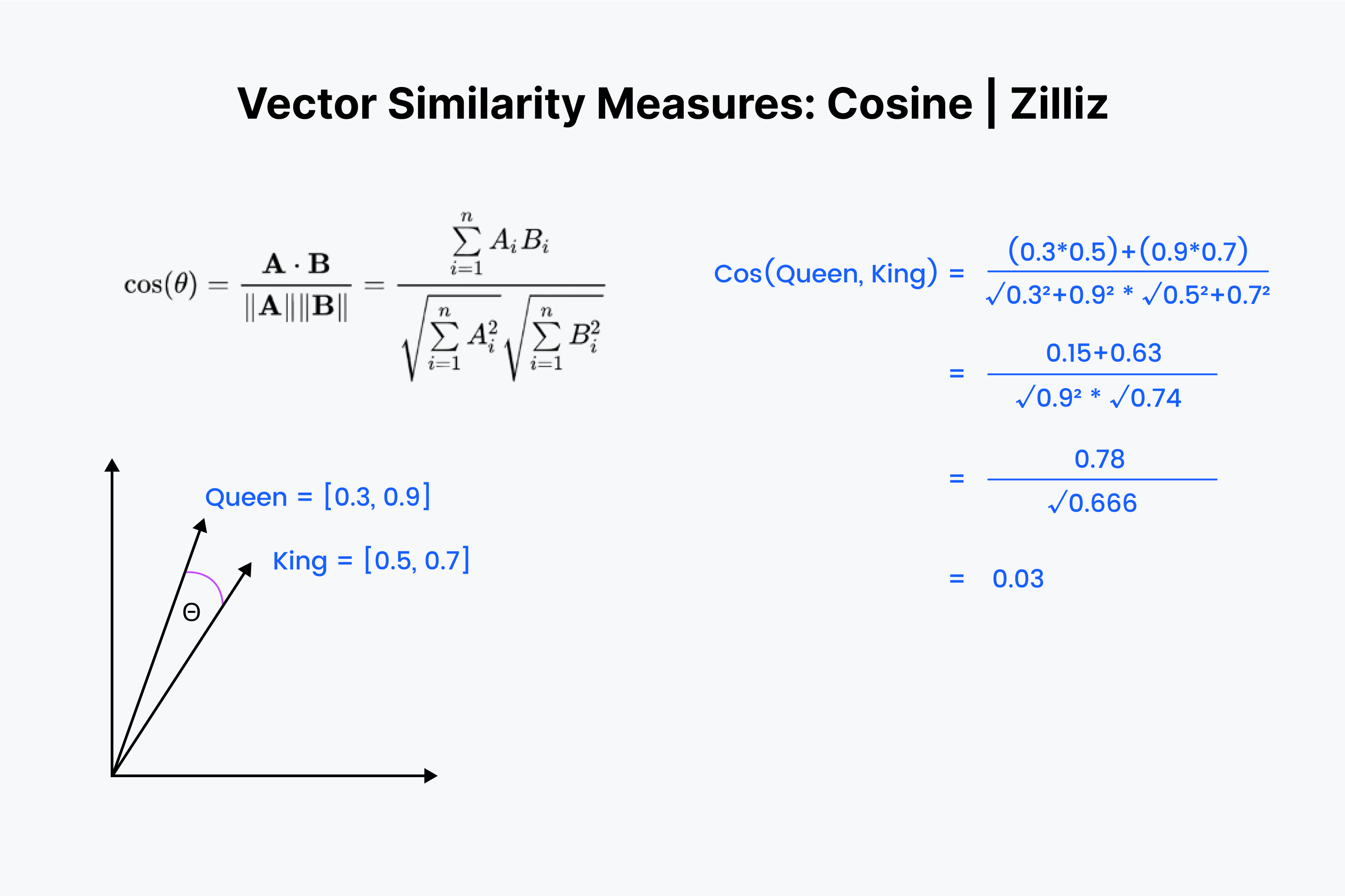
所以,我们知道了余弦相似度度量的是两个向量之间的夹角。让我们再次将我们的向量想象成一列数字。不过这次的过程稍微复杂一些。
我们再次将向量上下对齐。首先,将数字向下相乘,然后将所有结果相加。现在保存这个数字;称它为“x”。接下来,我们必须将向量中的每个数字平方,并将平方的结果相加。想象一下,对于两个向量,将每个向量中的数字按水平方向平方,之后相加求和。
接着,对这两个和求平方根,然后将它们相乘,称这个结果为“y”。我们将余弦距离的值定义为“x”除以“y”。
何时应该使用余弦相似度?
余弦相似度主要用于 NLP 应用。余弦相似度主要衡量的是语义方向的差异。如果您使用了归一化向量,余弦相似度等同于内积。
内积
内积是一个向量投影到另一个向量上的操作。内积的值是向量的长度拉伸出来的。两个向量之间的夹角越大,内积越小。它还会随着较小向量的长度而缩放。因此,当我们关心方向和距离时,我们使用内积。例如,你必须穿过墙壁跑到冰箱的直线距离。
内积是如何工作的?

内积应该看起来很熟悉。它只是余弦计算的前 ⅓ 部分。在你的脑海中将这些向量排成一行,向下相乘。然后将它们相加。这个过程测量了你和最近的点心之间的直线距离。
何时应该使用内积?
内积就像欧几里得距离和余弦相似度的混合体。当涉及到归一化数据集时,它等同于余弦相似度,因此内积适用于归一化或非归一化数据集。它是一个比余弦相似度更快的选项,也是一个更灵活的选项。
需要记住的一件事是,内积不遵循三角不等式。更大的长度(大的幅度)被优先考虑。这意味着我们在使用倒排文件索引或类似HNSW的图索引时应该小心使用内积。
译注:在倒排文件索引或HNSW(一种图索引方法)这类数据结构中,我们通常希望快速找到与给定查询最相似的项。如果使用内积作为相似性度量,那么更大的长度(或幅度)将优先考虑,这意味着具有较大长度的向量将被视为更相似,即使它们的实际方向可能相差很大。这可能导致不准确的搜索结果。
其他有趣的向量相似度或距离度量
上面提到的是对于向量嵌入最有用的三个向量度量方法。然而,它们并不是衡量两个向量之间距离的所有方法。以下是衡量两个向量之间距离或相似度的另外两种方法。
汉明距离

汉明距离可以应用于向量或字符串。对于我们的用例,让我们继续使用向量。汉明距离衡量了两个向量的 条目 之间的“差异”。例如,“1011”和“0111”的汉明距离为 2。
在向量嵌入方面,汉明距离只适用于二进制向量。浮点向量嵌入是由神经网络的倒数第二层输出的,由 0 到 1 之间的浮点数。例如 [0.24, 0.111, 0.21, 0.51235] 和 [0.33, 0.664, 0.125152, 0.1]。
正如你所看到的,两个向量嵌入之间的汉明距离几乎总是等于向量本身的长度。每个值的可能性太多了。这就是为什么汉明距离只能应用于二进制或稀疏向量。像 TF-IDF、BM25 或 SPLADE 这样的过程产生的向量就是这种类型的向量。
汉明距离适用于衡量两个文本之间的措辞差异、单词拼写差异或任何两个二进制向量之间的差异。但不适用于衡量向量嵌入之间的差异。
有趣的事实:汉明距离等于对两个向量执行 XOR 操作的结果的和。
杰卡德距离
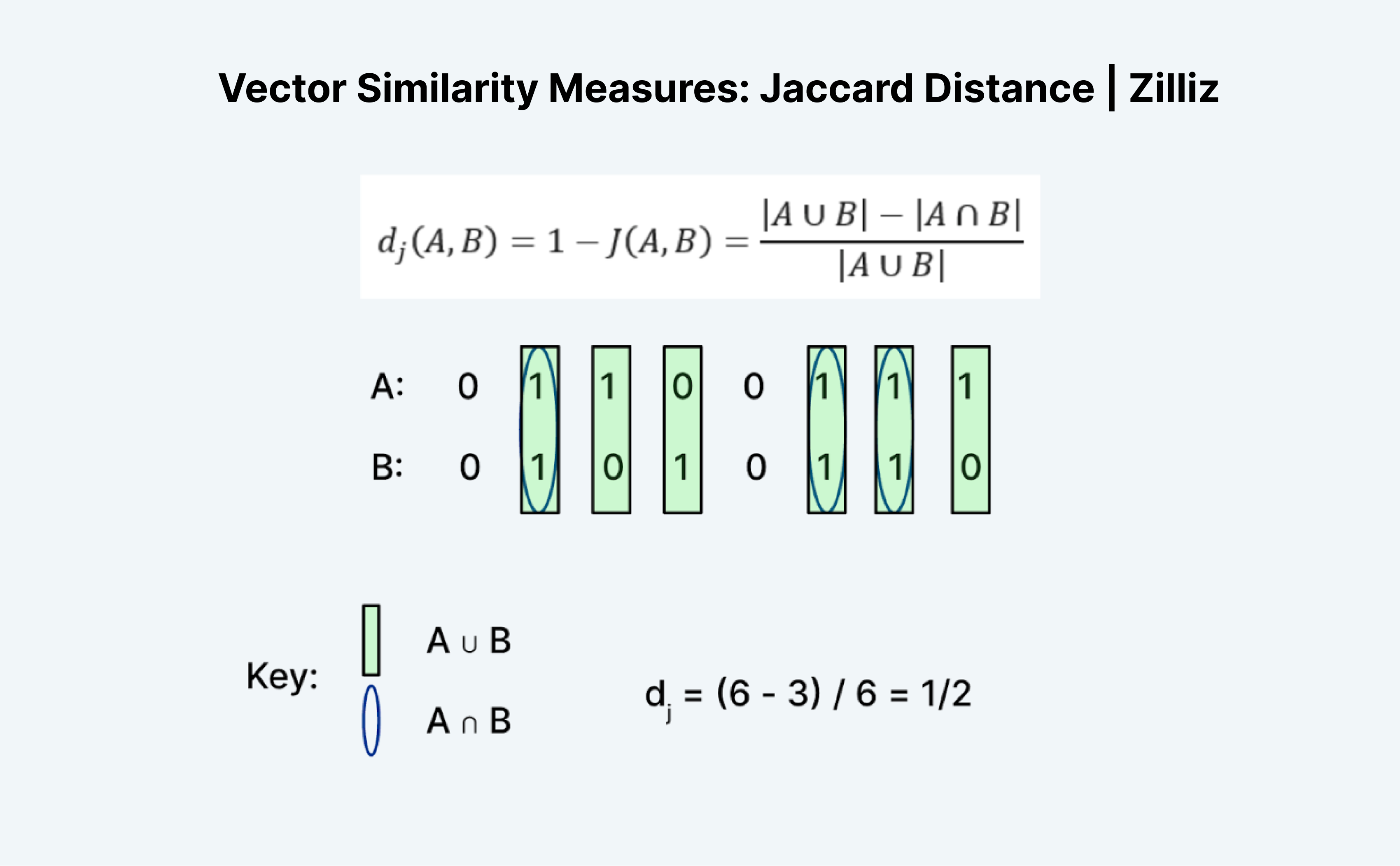
杰卡德距离是衡量两个向量相似性或距离的另一种方法。有趣的是,杰卡德有杰卡德 指数 和杰卡德 距离 两种方式。杰卡德距离等于 1 - 杰卡德系数,Milvus 中实现的是 Jaccard 距离度量。
计算杰卡德距离或指数是一项有趣的任务,因为乍一看它并不太有效。与汉明距离一样,杰卡德只适用于二进制数据。我发现传统的“并集”和“交集”形式令人困惑。我用逻辑上的方式理解它。它本质上就是 A “或” B 减去 A “且” B 再除以 A “或” B。
如上图所示,我们计算 A 或 B 为 1 的条目数作为“并集”,A 和 B 都为 1 的条目数作为“交集”。因此,A(01100111)和 B(01010110)的杰卡德指数为 ½。在这种情况下,杰卡德距离,1 减去杰卡德指数,也是 ½。
向量相似度搜索度量总结
在这篇文章中,我们了解了三种最有用的向量相似度搜索度量:L2(也称为欧几里得)距离、余弦距离和内积。每种度量都有不同的使用场景。欧几里得距离用于我们关心大小的差异。余弦用于我们关心方向的差异。内积用于我们关心大小和方向的差异。
查看这些视频,了解更多关于向量相似度度量的信息,或 阅读文档 了解如何在 Milvus 中配置这些度量。
- Vector Similarity Metrics: Cosine Similarity
- Vector Similarity Metrics: Inner Product
- Vector Similarity Metrics: L2 or Euclidean
